Exercises Part 3

1. Steady State Markov Process

   Find the steady state probabilites of the following Markov Process Solution

   

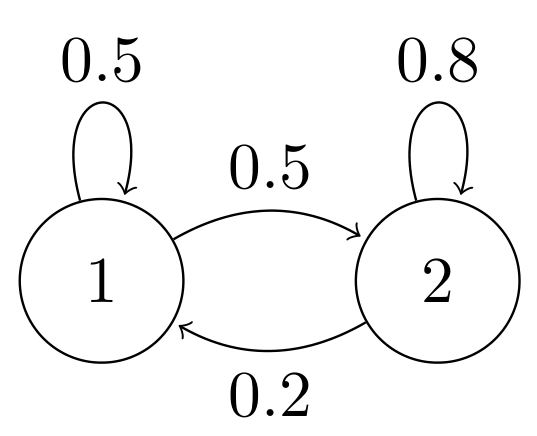
2. Absorption Probabilities

   Calculate the absorption probabilites for state $4$ and expected time to absortion from all states. (for absorption time, assume $p_{35}=0$ and $p_{32}=0.5$) Solution

   

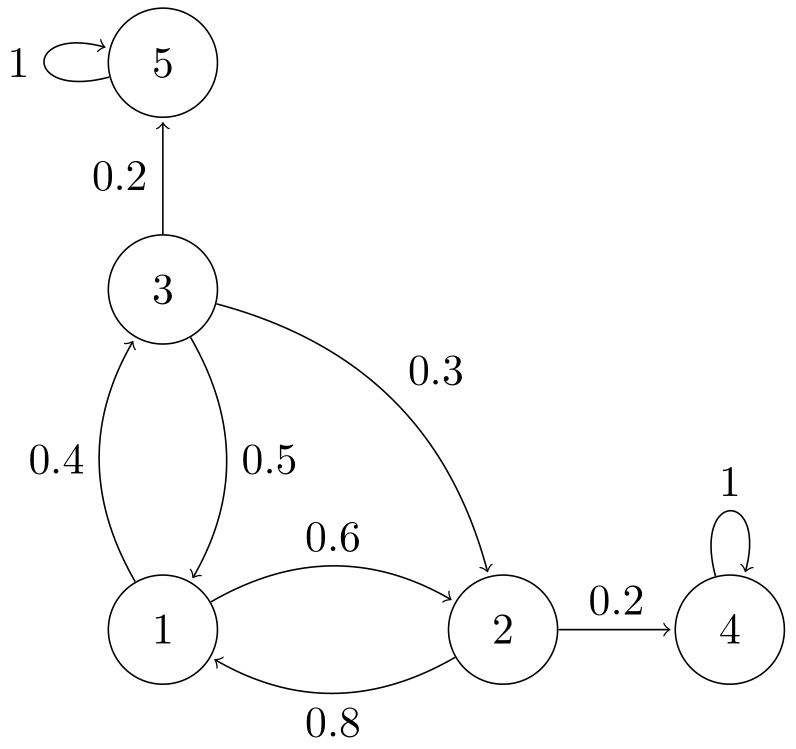
3. Selecting Courses with Markov Process

   

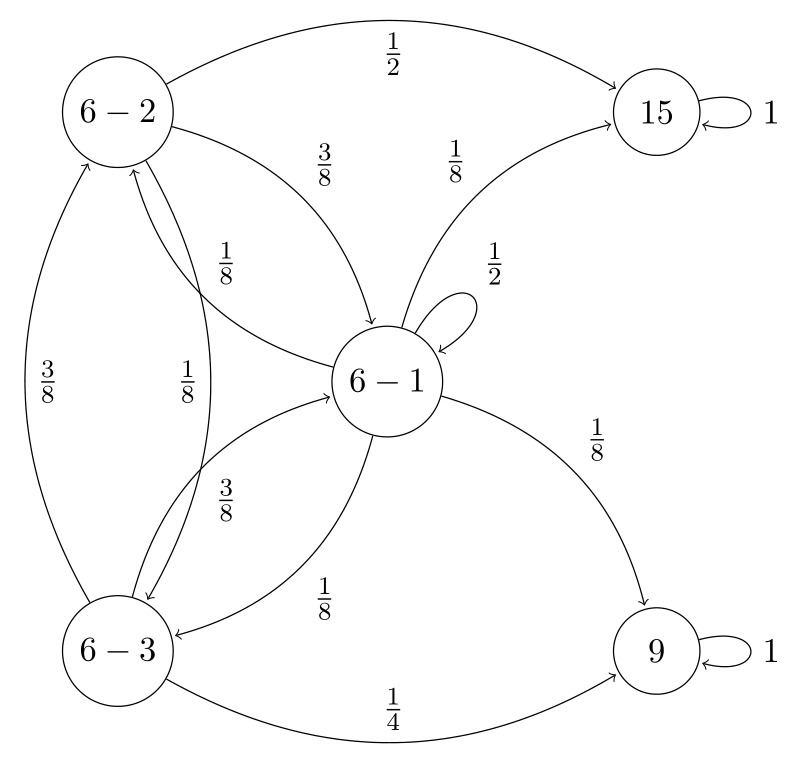
   Consider the above markov process for changing courses. The probability being in some course tomorrow given a course today is mentioned along the edges. Suppose we start with course 6-1 (Note that course 6 is the combination of courses 6-1, 6-2 and 6-3). Calculate the following

   1. $P($eventually leaving course 6$)$.

   2. $P($eventually landing in course 15$)$.

   3. $E[$number of days till leaving course 6$]$.

   4. At every switch for 6-2 to 6-1 or 6-3 to 6-1, we buy an ice cream (but a maximum of two). Calculate the $E[$number of ice creams before leaving course 6$]$.

   5. Suppose we end up in 15. What is the $E[$number of steps to reach 15$]$.

   6. Suppose we don’t want to take course 15. Accordingly, when in 6-1, we stay there with probability $1/2$ while other three options have equal probabilities. If we are in 6-2, probability of going to 6-1 and 6-3 are in the same ratio as before. Calculate the $E[$number of days until we enter course 9$]$.

   7. Assuming $$\begin{array}{rl}P(X_{n+1}=15|X_n=9)& =P(X_{n+1}=9|X_n=15)=P(X_{n+1}=15|X_n=15)\\ & =P(X_{n+1}=9|X_n=9)=1/2\end{array}$$ what is $P(X_n=15)$ and $P(X_n=9)$ far into the future.

   8. Suppose $$\begin{array}{rl}P(X_{n+1}=6-1|X_n=9)& =1/8\\ P(X_{n+1}=9|X_n=9)& =P(X_{n+1}=15|X_n=15)=7/8\end{array}$$ what is the $E[$number of days till return to 6-1$]$.

   Solution